Table of Contents
kalkulator całek
kalkulator całek krok po kroku znajduje funkcję pierwotną krok po kroku w odniesieniu do zmiennej, tj. x, y lub z. Ten kalkulator integracji online obsługuje również górną i dolną granicę w przypadku pracy z minimalną lub maksymalną wartością interwałów.
Za pomocą tego kalkulatora całkowego możesz wykonać krok po kroku obliczenia:
- Określona całka
- Całka nieoznaczona
Potrafi znaleźć całki funkcji logarytmicznych oraz funkcji trygonometrycznych. To narzędzie ocenia funkcję wejściową i odpowiednio wykorzystuje reguły całkowania do oceny całek dla powierzchni, objętości itp.
Jak działa kalkulator pierwotny?
Narzędzie to wykorzystuje parser, który analizuje daną funkcję i przekształca ją w drzewo. Komputer interpretuje drzewo, aby poprawnie ocenić kolejność operacji i odpowiednio implementuje reguły integracji.
Możesz znaleźć pierwotną (całkę) dowolnej funkcji, wykonując poniższe czynności.
- Wybierz opcję do końca lub na czas nieokreślony.
- Wprowadź funkcję w odpowiednim polu wejściowym.
- Kliknij przycisk Załaduj przykład, jeśli chcesz użyć przykładowego przykładu.
- Określ zmienną. Domyślnie jest ustawiony jako x.
- Wpisz górną i dolną granicę graniczną, jeśli powyżej wybrałeś całkę określoną.
- Kliknij przycisk Oblicz. Otrzymasz wynik z obliczeń krok po kroku.
Rozwiązanie możesz pobrać, klikając ikonę.
Co to jest całka?
Całkę można zdefiniować jako,
„Integral przypisuje liczby do funkcji w sposób, który opisuje objętość, powierzchnię, przemieszczenie i inne pomysły, które powstają w wyniku łączenia nieskończonych danych”.
Proces znajdowania całek nazywamy integracją. Całka jest również określana jako pierwotna, ponieważ jest odwrotną operacją wyprowadzania.
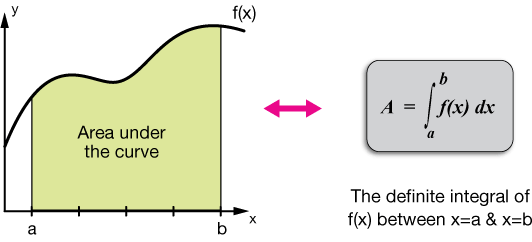
Całkowanie, obok różniczkowania, jest podstawową operacją rachunku różniczkowego i służy jako narzędzie do rozwiązywania problemów matematyczno-fizycznych, obejmujących m.in. długość krzywej, objętość bryły, pole dowolnego kształtu.
Całka funkcji f(x) względem zmiennej rzeczywistej x w przedziale [a, b] jest zapisana jako:
\(\int _a^bf\left(x\right)dx\:\)
Jak znaleźć funkcję pierwotną (całkę)?
Zobacz poniższe przykłady, aby dowiedzieć się, jak obliczać całki oznaczone i nieoznaczone przy użyciu reguł całkowania.
Przykład 1
Określona całka
Oceniać \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Rozwiązanie:
- Zastosuj zasadę sumy. Napisz znak integracji z każdą zmienną osobno.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
Powyższą funkcję można zapisać jako:
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Zastosuj regułę potęgi do obu wyrażeń, aby ocenić wykładniki.
Zasada mocy: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Zastosuj regułę stałą, która pozostawia C z końcowym wyrażeniem.
Stała zasada:
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Przykład nr 2
Całka nieoznaczona
Oceniać \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Rozwiązanie:
- Zmień kolejność funkcji jak poniżej.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Zastosuj regułę sum do funkcji.
Reguła sumy: \(\int \left(f+g\right)dx=\int f\:dx+\int g\:dx\)
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\)------ Równ. 1
- Rozwiąż każde wyrażenie w powyższej funkcji, implementując reguły integralne.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\)
\(\int xdx=\frac{x^2}{2}\:\)
- Podstaw wartości rozwiązania w równaniu 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
C jest dodawane ze względu na stałą regułę.
- W razie potrzeby uprość równanie.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
Często zadawane pytania
Jaka jest całka z 1/x?
Całka z 1/x jest wartością bezwzględną: ln (|x|) + C. Jest to standardowa wartość całkowania.
Jaka jest różnica między całką oznaczoną a nieoznaczoną?
Całka oznaczona oznacza liczbę, gdy górna i dolna granica są stałe. Natomiast całka nieoznaczona to rodzina funkcji, których pochodne to f. Różnica między tymi dwiema funkcjami jest stała.
Jaka jest funkcja pierwotna tan(x) dx?
Pochodną tan(x) dx jest,
tan x = - ln |cos x| + C