Tabla de contenido
Calculadora de antiderivadas con pasos
Calculadora de antiderivadas encuentra la antiderivada de una función paso a paso con respecto a una variable, es decir, x, y o z. Esta calculadora de integración en línea también es compatible con el límite superior y el límite inferior en caso de que esté trabajando con un valor mínimo o máximo de intervalos.
Con esta calculadora integral, puede obtener cálculos paso a paso de:
- Integral definida
- Integral indefinida
Puede encontrar las integrales de funciones logarítmicas y trigonométricas. Esta herramienta evalúa la función de entrada y usa reglas integrales en consecuencia para evaluar las integrales para el área, el volumen, etc.
¿Cómo funciona la calculadora de antiderivadas?
Esta herramienta utiliza un analizador que analiza la función dada y la convierte en un árbol. La computadora interpreta el árbol para evaluar correctamente el orden de las operaciones e implementa las reglas de integración apropiadamente.
Puede encontrar la antiderivada (integral) de cualquier función siguiendo los pasos a continuación.
- Seleccione la opción definida o indefinida.
- Ingrese la función en el cuadro de entrada dado.
- Haga clic en el botón Cargar ejemplo si desea utilizar un ejemplo de muestra.
- Especifique la variable. Se establece como x por defecto.
- Ingrese el límite superior e inferior si eligió integral definida arriba.
- Presiona el botón Calcular. Obtendrá el resultado con cálculos paso a paso.
Puede descargar la solución haciendo clic en el icono.
¿Qué es una integral?
Una integral se puede definir como,
"Integral asigna números a funciones de una manera que describe el volumen, el área, el desplazamiento y otras ideas que surgen al combinar datos infinitesimales".
El proceso de encontrar integrales se llama integración. Integral también se conoce como antiderivada porque es una operación inversa de derivación.
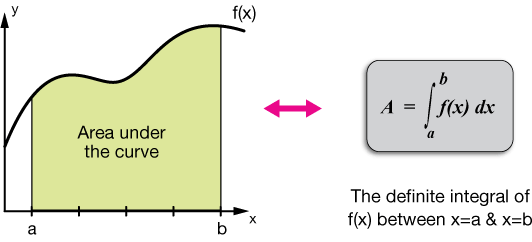
Junto con la diferenciación, la integración es una operación esencial del cálculo y sirve como herramienta para resolver problemas matemáticos y físicos relacionados con la longitud de una curva, el volumen de un sólido y el área de una forma arbitraria, entre otros.
La integral de una función f(x) con respecto a una variable real x en un intervalo [a, b] se escribe como:
\(\int _a^bf\left(x\right)dx\:\)
¿Cómo encontrar la Antiderivada (Integral)?
Vea los siguientes ejemplos para aprender cómo evaluar integrales definidas e indefinidas usando reglas de integración.
Ejemplo 1
Integral definida
Evaluar \(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:\)
Solución:
- Aplicar la regla de la suma. Escribe el signo de integración con cada variable por separado.
\(\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
La función anterior se puede escribir como: Aplique la regla de la potencia en ambas expresiones para evaluar los exponentes.
\(=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:\)
- Aplique la regla de la potencia en ambas expresiones para evaluar los exponentes.
Regla de poder: \(\int x^ndx=\frac{x^{n+1}}{n+1}\:\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0\)
- Aplicar el teorema fundamental del cálculo.
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}\)
\(\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167\)
Ejemplo # 2
Integral indefinida
Evaluar \(\int \left(3x^2−6x+2sin\left(x\right)\right)dx\)
Solución:
- Reorganice la función como se muestra a continuación.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx\)
- Aplicar la regla de la suma a la función.
\(\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx\) ...Ecuación 1
- Resuelva cada expresión en la función anterior implementando reglas integrales.
\(\int sin\left(x\right)dx=-cos\left(x\right)\) ... d/dx sin(x)=cos(x)
\(\int x^2dx=\frac{x^3}{3}\:\) ... regla de potencia aplicada
\(\int xdx=\frac{x^2}{2}\:\) ... Regla de potencia aplicada. Consulte el ejemplo anterior
- Sustituya los valores de resolución en la Ecuación 1.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C\)
Se agrega C debido a la regla constante.
- Simplifica la ecuación si es necesario.
\(\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C\)
preguntas frecuentes
¿Cuál es la integral de 1/x?
La integral de 1/x es un valor absoluto: ln (|x|) + C. Es un valor de integración estándar.
¿Cuál es la diferencia entre integral definida e indefinida?
Una integral definida denota un número cuando los límites superior e inferior son constantes. Por otro lado, la integral indefinida es una familia de funciones cuyas derivadas son f. La diferencia entre las dos funciones es una constante.
¿Cuál es la antiderivada de tan(x) dx?
La antiderivada de tan(x) dx es,
tan x = - ln |cos x| + C