Calculadora Antiderivada

Para usar a calculadora antiderivada, selecione o tipo (definido ou indefinido), insira a função, preencha as caixas de entrada necessárias e pressione o botão calcular

Definite

Indefinite

Enter Function

⌨

Wrt: ⓘ

Upper bound:

Lower bound:

inf = \infty , pi = π and -inf = -\infty

This will be calculated

2 3

$${ {\color{gray} ∫}(cos(x)+x/2 ) dx}$$

Mobile Apps

Download our Android app from Google Play Store and iOS app from Apple App Store.

Table of Contents

Calculadora antiderivada com passos

Calculadora de antiderivadas encontra a primitiva de uma função passo a passo em relação a uma variável, ou seja, x, y ou z. Esta calculadora de integração online também suporta limite superior e limite inferior caso você esteja trabalhando com valores mínimos ou máximos de intervalos.

Com esta calculadora integral, você pode obter cálculos passo a passo de:

Integral definida
Integral indefinida

Ele pode encontrar as integrais de funções logarítmicas e trigonométricas. Esta ferramenta avalia a função de entrada e usa regras de integral de acordo para avaliar as integrais para a área, volume, etc.

área sob a curva

Como funciona a calculadora antiderivada?

Essa ferramenta usa um analisador que analisa a função fornecida e a converte em uma árvore. O computador interpreta a árvore para avaliar corretamente a ordem das operações e implementa as regras de integração apropriadamente.

Você pode encontrar a primitiva (integral) de qualquer função seguindo as etapas abaixo.

Selecione a opção definitiva ou indefinida.
Insira a função na caixa de entrada fornecida.
Clique no botão Carregar Exemplo se desejar usar um exemplo de amostra.
Especifique a variável. É definido como x por padrão.
Insira o limite superior e inferior se você escolheu a integral definida acima.
Aperte o botão Calcular. Você obterá o resultado com cálculos passo a passo.

Você pode baixar a solução clicando no ícone.

O que é uma Integral?

Uma integral pode ser definida como,

"Integral atribui números a funções de uma maneira que descreve volume, área, deslocamento e outras ideias que surgem ao combinar dados infinitesimais."

O processo de encontrar integrais é chamado de integração. A integral também é chamada de antiderivada porque é uma operação reversa da derivação.

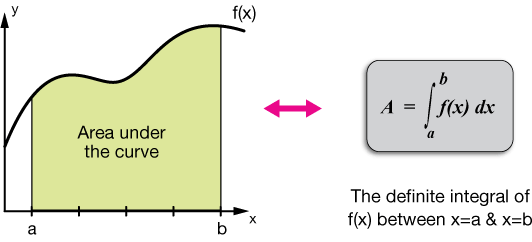
fórmula integral definida

Juntamente com a diferenciação, a integração é uma operação essencial do cálculo e serve como uma ferramenta para resolver problemas de matemática e física envolvendo o comprimento de uma curva, o volume de um sólido e a área de uma forma arbitrária, entre outros.

A integral de uma função f(x) em relação a uma variável real x em um intervalo [a, b] é escrita como:

$\int _a^bf\left(x\right)dx\:$

Como encontrar a Antiderivada (Integral)?

Veja os exemplos abaixo para aprender como calcular integrais definidas e indefinidas usando regras de integração.

Exemplo 1

Integral definida

Avalie $\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:$

Solução:

Aplique a regra da soma. Escreva o sinal de integração com cada variável separadamente.

$\int _0^1\sqrt{x}dx+\int _0^1x^{\frac{1}{3}}dx\:$

A função acima pode ser escrita como:

$=\int _0^1x^{\frac{1}{2}}dx+\int _0^1x^{\frac{1}{3}}dx\:$

Aplique a regra da potência em ambas as expressões para calcular os expoentes.

Regra de energia: $\int x^ndx=\frac{x^{n+1}}{n+1}\:$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]^1_0+\left[\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}\right]^1_0$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^1_0+\left[\frac{x^{\frac{4}{3}}}{\frac{4}{3}}\right]^1_0$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\left[\frac{2x^{\frac{3}{2}}}{3}\right]^1_0+\left[\frac{3x^{\frac{4}{3}}}{4}\right]^1_0$

Aplique a regra constante que deixa C com a expressão final.

Regra constante:

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[x^{\frac{3}{2}}\right]^1_0+\frac{3}{4}\left[x^{\frac{4}{3}}\right]^1_0$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1^{\frac{3}{2}}-0^{\frac{3}{2}}\right]+\frac{3}{4}\left[1^{\frac{4}{3}}-0^{\frac{4}{3}}\right]$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}\left[1-0\right]+\frac{3}{4}\left[1-0\right]$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{2}{3}+\frac{3}{4}$

$\int _0^1\left(\sqrt{x}+\sqrt[3]{x}\right)dx\:=\frac{17}{12}=1.4167$

Exemplo # 2

Integral indefinida

Avalie $\int \left(3x^2−6x+2sin\left(x\right)\right)dx$

Solução:

Reorganize a função conforme abaixo.

$\int \left(2sin\left(x\right)+3x^2−6x\right)dx$

Aplique a regra de soma à função.

Regra da soma: $\int \left(f+g\right)dx=\int f\:dx+\int g\:dx$

$\int \left(2sin\left(x\right)+3x^2−6x\right)dx=2\int sin\left(x\right)dx+3\int x^2dx−6\int xdx$

Resolva cada expressão na função acima implementando regras integrais.

$\int sin\left(x\right)dx=-cos\left(x\right)$ ... d/dx sin(x)=cos(x)

$\int x^2dx=\frac{x^3}{3}\:$

$\int xdx=\frac{x^2}{2}\:$

Substitute the solve values in Equation 1.

$\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+\frac{3x^3}{3}−\frac{6x^2}{2}+C$

C is added because of the constant rule.

Simplify the equation if needed.

$\int \:\left(2sin\left(x\right)+3x^2−6x\right)dx=-2cos\left(x\right)+x^3−3x^2+C$

Perguntas frequentes

Qual é a integral de 1/x?

A integral de 1/x é um valor absoluto: ln (|x|) + C. É um valor de integração padrão.

Qual é a diferença entre integral definida e indefinida?

Uma integral definida denota um número quando os limites superior e inferior são constantes. Por outro lado, a integral indefinida é uma família de funções cuja derivada são f. A diferença entre as duas funções é uma constante.

Qual é a primitiva de tan(x) dx?

A primitiva de tan(x) dx é,

tan x = - ln |cos x| +C